Plannen vermogensbelasting 2015: wie betaalt meer, wie betaalt minder?

Update September 2016: grafiek voor 2017 toegevoegd waarin de plannen (in gewijzigde vorm) daadwerkelijk in werking zullen treden.

Nieuwe plannen voor de vermogensbelasting:

• Nog steeds 30% belasting over een fictief rendement
• Het fictieve rendement wordt nu bepaald aan de hand van rentes van de afgelopen 5 jaar (vergelijkbaar met de berekening van de studieschuldrente)
• Het fictieve rendement wordt progressief, wat in veel gevallen realistischer zal zijn (hoe meer vermogen, hoe meer risico je je kunt permitteren en dus hoe meer rendement over de lange termijn):
  • Schijf 0: t/m € 25k belastingvrij (is nu voor 2015 € 21.330)
  • Schijf 1: € 25k t/m €125k 2,7%
  • Schijf 2: € 125k t/m €1M 4,7%
  • Schijf 3: vanaf € 1M 5,5%

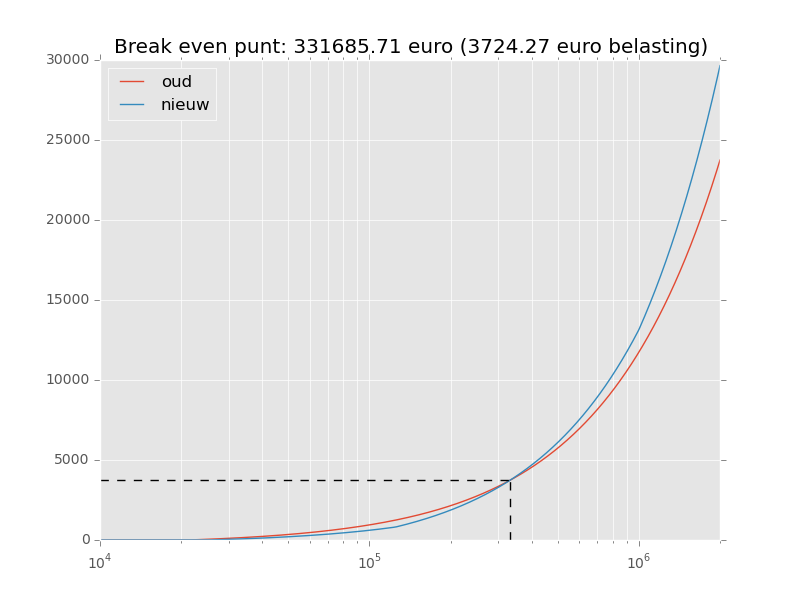
Dit kunnen we vergelijken met de huidige vlaktaks van 30% op 4% fictief rendement. Bij welke vermogens betaal je minder en bij welke betaal je meer in dit nieuwe tarievenschema?

#!/usr/bin/env python
import numpy as np
import scipy.optimize as opt
import matplotlib.pyplot as plt
plt.style.use('ggplot')

b_nieuw = lambda v: 0.3 * ( (0.027 * np.clip(v-25000, 0, 100000)) + (0.047 * np.clip(v-125000, 0, 875000)) + (0.055 * np.max((v-1e6, np.zeros_like(v)), axis=0)) )
b0 = lambda v: 0.3*(0.04 * np.max((np.zeros_like(v), ( v - 21330 )), axis=0) )
x = np.linspace(0, 2e6, 100000)

d_b = lambda v: np.abs(b0(v) - b_nieuw(v))

break_even = opt.fmin(d_b, 200000)[0]

plt.semilogx(x, b0(x), label='oud')
plt.semilogx(x, b_nieuw(x), label='nieuw')

plt.xlim(10000, 2e6)

ylim = plt.ylim()
plt.semilogx((break_even,)*2, (ylim[0], b0(break_even)), 'k--')
plt.semilogx((plt.xlim()[0], break_even), (b0(break_even), b0(break_even)), 'k--')

plt.title(('Break even punt: {0:.2f} euro ({1:.2f} euro belasting)'
           ).format(break_even, b0(break_even)))

plt.grid(b=True, which='both')

plt.legend(loc='best')
plt.show()

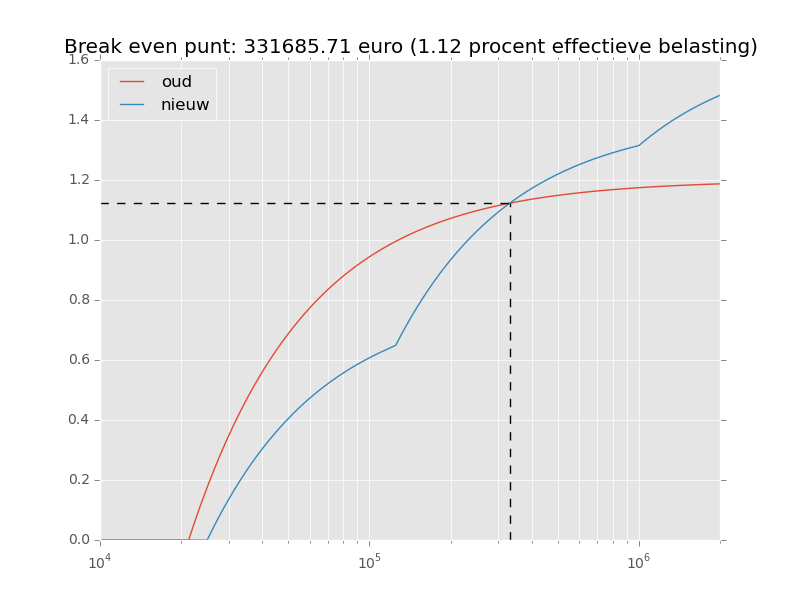
Het effectieve percentage belasting dat je over je totale bedrag betaalt ziet er als volgt uit:

# effectieve rente
effectief_0 = b0(x) / x * 100
effectief_nieuw = b_nieuw(x) / x * 100

plt.figure()

plt.semilogx(x, effectief_0, label='oud')
plt.semilogx(x, effectief_nieuw, label='nieuw')

plt.xlim(10000, 2e6)

ylim = plt.ylim()
plt.semilogx((break_even,)*2, (ylim[0], b0(break_even) / break_even * 100), 'k--')
plt.semilogx((plt.xlim()[0], break_even), (b0(break_even) / break_even * 100, b0(break_even) / break_even * 100), 'k--')

plt.title(('Break even punt: {0:.2f} euro ({1:.2f} procent effectieve belasting)'
           ).format(break_even, b0(break_even) / break_even * 100))

plt.grid(b=True, which='both')

plt.legend(loc='best')

plt.show()

Update september 2016:

De plannen gaan in enigszins gewijzigde vorm in 2017 in werking. Voor mensen met een flink vermogen zijn de aanpassingen nog iets minder gunstig dan de oorspronkelijke plannen; zie de figuur hieronder.

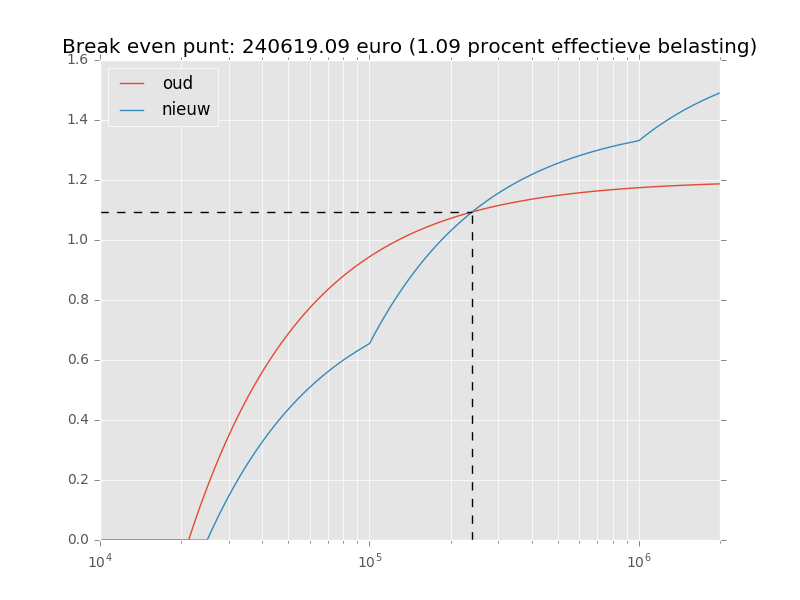
Hiervoor kun je in het bovenste stukje Python b_nieuw vervangen met de volgende regels.

# versie 2017:
perc1 = 0.0163
perc2 = 0.055
tarief1 = 0.67 * perc1 + 0.33 * perc2
tarief2 = 0.21 * perc1 + 0.79 * perc2
tarief3 = perc2
b_nieuw = lambda v: 0.3 * ((tarief1 * np.clip(v - 25000, 0, 75000)) +
                           (tarief2 * np.clip(v - 100000, 0, 900000)) +
                           (tarief3 * np.max((v - 1e6, np.zeros_like(v)), axis=0)))